Simplificar una expresión algebraica con paréntesis y productos supone aplicar la propiedad distributiva del producto respecto de la suma y de la resta. La igualdad (1) enuncia la propiedad distributiva respecto de la suma y la igualdad (2) enuncia la propiedad distributiva respecto de la resta:
(1) k(a + b) = ka + kb
(2) k(a – b) = ka – kb
Para simplificar, unas veces convertiremos un producto en una suma, y otras convendrá lo contrario, es decir, sacar factor común en la expresión.
2) MULTIPLICACIÓN
Para la multiplicación algebraica se mantienen las mismas leyes que para la multiplicación aritmética, las cuales son:
Ley de signos: el resultado es negativo si la cantidad de factores negativos es impar, de lo contrario es positivo.
(+) (+) = +
(-) (-) = +
(+) (-) = -
(-) (+) = -
Ley de exponentes: el producto de dos o más potencias de la misma base es igual a la base elevada a la suma de las potencias.
(xm) (xn) = xm + n
Ley conmutativa: el orden de los factores no altera el producto
(x) (z) (y) = (y) (z) (x) = (z) (x) (y) = xyz
Ley de los coeficientes: el coeficiente del producto de dos o más expresiones algebraicas es igual al producto de los coeficientes de los factores.
(4x) (5y) = 4 · 5 · x · y = 20xy
Multiplicación de monomios
Se le llama multiplicación de monomios a la multiplicación de un solo término por otro término
Reglas:
Se multiplica él termino del multiplicando por él termino del multiplicador.
Se suman los exponentes de las literales iguales.
Se escriben las literales diferentes en un solo término resultado.
Se coloca el signo de acuerdo con las reglas de los signos vistas anteriormente.
Cuando existen multiplicación más de dos monomios resulta sencillo multiplicar uno a uno los factores para obtener el resultado.
Ejemplos:
En el último ejemplo se multiplican primero los dos primeros factores entre si, sin tocar el resto, luego se multiplica este resultado por el tercer factor, por último se multiplicó este segundo resultado por el cuarto factor obteniéndose el resultado final.
3) DIVISION
1 1
3.(x - 2)
Se cambia la división por multiplicación, y se invierte la segunda fracción. Luego se procede como en una multiplicación de fracciones.
Y si lo piden, aclaremos que la simplificación vale para todo x ≠ -2 y x ≠ 5.
4) SUMAS Y RESTAS
(Suma de fracciones con igual denominador)
Y si lo piden, aclaremos que la simplificación vale para todo x ≠ -2.
(Resta de fracciones con igual denominador)
Las dos fracciones tienen el mismo denominador. El denominador común es ese denominador, y se suman los numeradores. Si el segundo numerador tiene más de un término, hay que ponerlo entre paréntesis para restarlo, ya que es signo menos afectará a todos los términos.
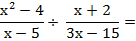
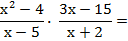
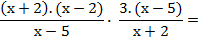
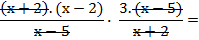
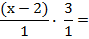
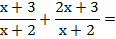
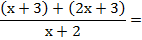
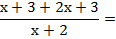
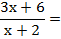
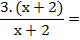
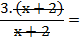
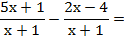
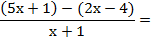
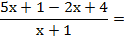
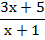
No hay comentarios:
Publicar un comentario